The Parallel Postulate Decomposed

A short ~5min talk I gave based on the prompt:

"What was Euclid's own contribution to mathematics?"

I thought this question was pretty vague so I took it as a way to talk about any number of things. I thought to myself, one of the many things named after Euclid which also has a converse named somewhat after him: Euclidean and non-Euclidean geometry.

To lay the groundwork, the parallel postulate states the following:

"If a line segment intersects two straight lines forming two interior angles on the same side that are less than two right angles, then the two lines, if extended indefinitely, meet on that side on which the angles sum to less than two right angles."

What this generalizes to is the idea that there is only one parallel line given another line (remember in euclidean geometry there's no distance measurement so a line with the same slope a bit farther relative to another line isn't counted as unique). This is correct in the case of doing geometry on a flat plane, the one we're mostly familiar with, it holds up. However, one can also imagine doing geometry on curved 2-dimensional surfaces. For instance, a sphere! Witness...

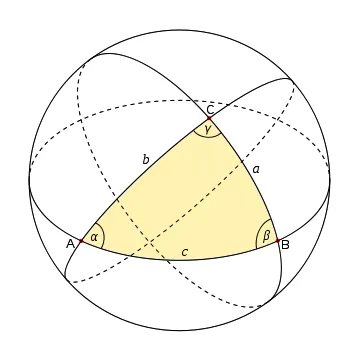
This image is a good representation of one of the ways the parallel postulate fails in spherical geometry. For those familiar, you'll know the proof that the interior angles of a triangle depends on the parallel postulate. For those unfamiliar, just know that Euclid and The Ancients^(tm) knew that the parallel postulate was qualitatively different from the other axioms and therefore proved the first like 32(?) theorems of The Elements without it. So why does this picture show it particularly well? The interior angles of that triangle are clearly greater than 180 degrees when all added together! Okay maybe not clearly... but trust me you can draw cases where it's clearer. And this one is likely still above 180. Anyway.

For another breakdown of the issue here, imagine geometry on a sphere, with lines defined as "great circles" around the globe. Meaning a line would go all around the sphere following the circumference in any direction, like drawing a bunch of different equators. Now with that definition, try drawing two parallel lines. It doesn't work!

Now hyperbolic geometry is geometry on a hyperbolic plane. Easy right? Like looking down on a round tipped cone. A line here is a line which is orthogonal (fancy/general way of saying perpendicular) to the borders of the plane space you're working in. In this case, again all axioms besides the parallel postulate hold and this is a consistent geometrical model. However, there's an infinite amount of parallel lines. Observe below a line and its perpendiculars:

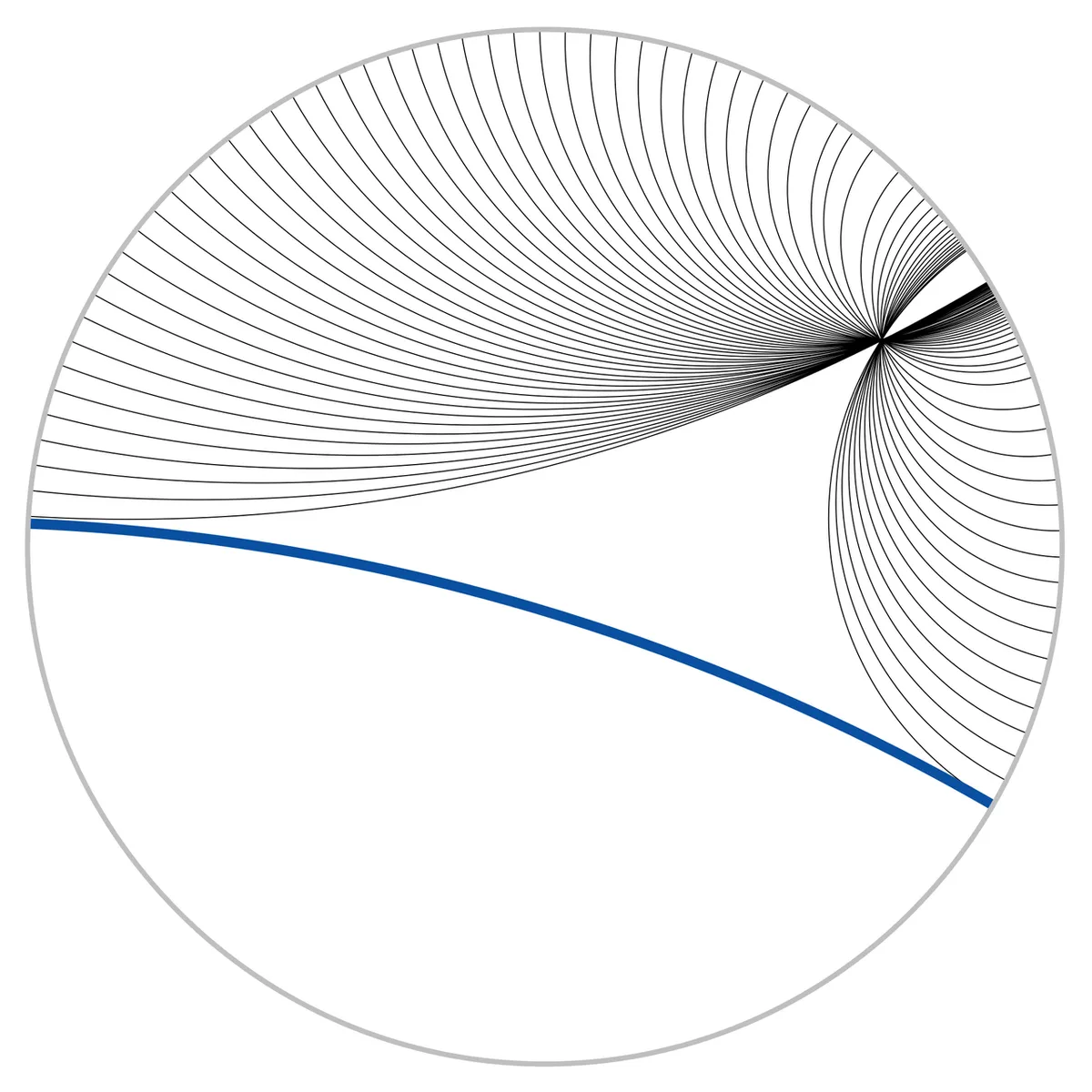
Playfair's Axiom

"In a plane through a point there is at most one line which never intersects the given line"

Now this is a very elegant way to wrap up this whole issue. It accounts for the spherical case, "at most one" can include zero. And the hyperbolic case is handled with help from Euclid's other axioms. I may try to write some more about that later. This solution is quite attractive as it keeps the amount of axioms the same, I just didn't like that it utilized the concept of a plane, something the Greeks were likely not considering seperate from 3D space, but likely rather an aspect of it. (Bird eye view etc.) For that reason I didn't just do my talk on Playfair's axiom.

The Lotschnittaxiom

"Perpendiculars raised on either side of a right angle will intersect"

The axiom itself is pretty weak, it seems to be a sort of general version of the rectangle axiom which states perpendiculars raised on either leg of a right angle will form another right angle, together making a rectangle. However let's be careful to not use that one despite seeming more intuitive, that axiom is equivalent to the parallel postulate and thus fails in many of the same ways.

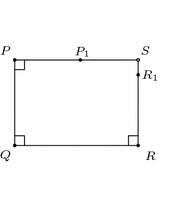
Aristotle's Axiom

If XOY is an acute angle and AB is any segment on OX (or any line segment in general), then there exists a point P on the ray OY and a point Q on the ray OX, such that PQ is perpendicular to OX and PQ > AB.

This one was hard to parse for me for a bit. What helped was thinking of the segment AB more as just its length. Then it's a bit easier to see Aristotle's axiom is more of a statement on the infinitely diverging ends of the legs of an acute angle. AKA: Having an acute angle between two lines means you can pick a third side with any length and create a right triangle with it.

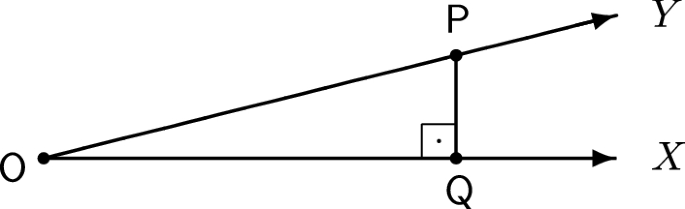
Putting Them Together

These two axioms form kind of a tag team on non-euclidean geometry. The Lotschnittaxiom handles the hyperbolic case and Aristotle's axiom handles the spherical case. For the hyperbolic case, see below a clear example of perpendiculars raised on legs of a right angle which do not meet.

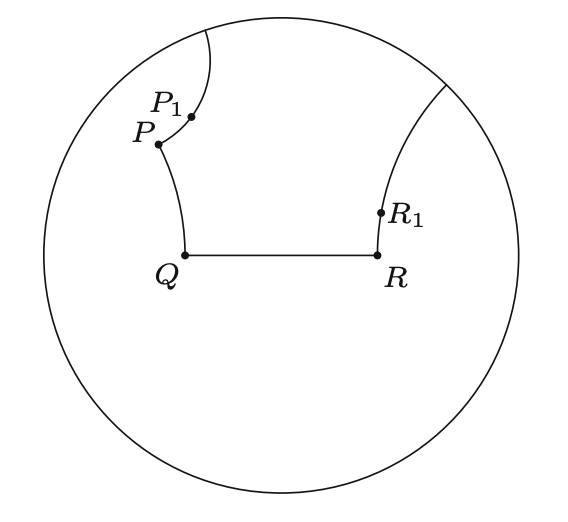
To demonstrate how Aristotle handles the spherical case, see (below) this acute angle on a sphere. The first thing to notice is that the ends of an acute angle meet again. That alone should tell you how you can't form a right triangle with any side length using this acute angle. In general, notice that a line segment (the longest one) on a sphere can be decribed as the circumference of the sphere, and the side of a right triangle on a sphere can never be as long as the circumference of the sphere itself.

That's it for this talk! Thanks for reading, hope some of this made sense to non-math people.
~Bone🦴